算法性能分析

本博客的内容是对代码随想录中算法性能分析和hello算法 计算复杂度的笔记

两个维度：

时间
空间

时间复杂度

时间复杂度是一个定性描述算法运行时间的函数。
在分析算法的时间复杂度的过程中，通过估算算法的操作单元数量来估算程序消耗的时间

假设算法的问题规模为n，那么操作单元数量便用函数f(n)来表示，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这称作为算法的渐近时间复杂度，简称时间复杂度，记为 \(O(f(n))\)。

时间复杂度常见类型排序

当输入数据大小为n时，常见时间复杂度排序（从低到高）：

\[ O(1) < O(log n)<O(n)<O(nlogn)<O(n^{2})<O(2^{n}<O(n!)\] \[常数阶<对数阶<线性对数阶<平方阶<指数阶<阶乘阶\]

时间复杂度常见类型.
from:hello算法

其中O(f(n))中的大O用来表示算法最坏情况运行时间的上界，即对任意数据输入的运行时间的上界

不同数据规模的差异

不同算法的时间复杂度在不同的数据输入规模下是有差异的。如下图所示：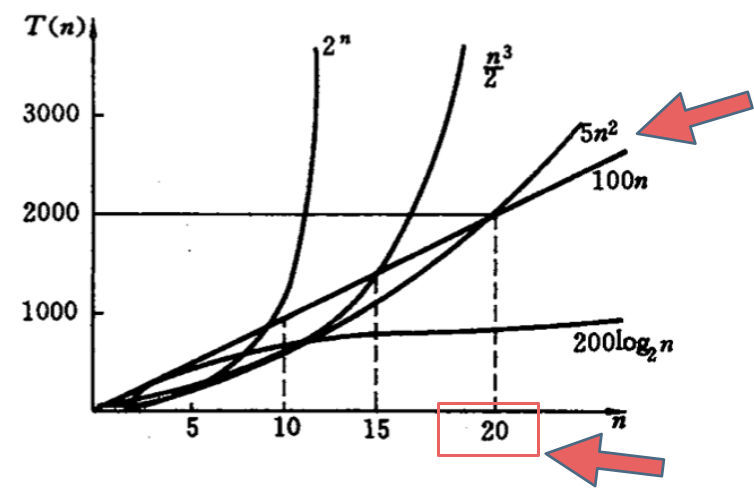

在不同数据输入规模下不同算法的时间复杂度.
from:代码随想录

当n大于20之后常数项系数就不再起决定性作用了。所以我们讨论时间复杂度时，通常都是省略了常数项系数。但是在实际应用中，我们决定使用哪个算法，需要考虑数据规模

复杂表达式化简

时间复杂度化简步骤：去除加法常数项->去掉常数系数->保留最高项 例子： \[O(2 n^{2} + 10n + 1000)\] \[\downarrow\] \[O(2 n^{2} + 10n)\] \[\downarrow\] \[O(n^{2} + n)\] \[\downarrow\] \[O(n^{2})\]

空间复杂度

空间复杂度统计算法使用内存空间随着数据量变大的增长趋势。
Ps:

空间复杂度是考虑程序运行时占用内存的大小，而不是可执行文件的大小。
空间复杂度不能精准预估程序的内存使用大小，很多因素会影响程序真正内存使用大小，例如编译器的内存对齐，编程语言容器的底层实现等等这些都会影响到程序内存的开销。所以空间复杂度是预先大体评估程序内存使用的大小。

例子：

j = 0;
for i in range(n):
    j++

从上面的代码就可以看出来，随着n的变化，内存的需求不会发生改变始终为\(O(1)\)

1
2
3

list = []
for i in range n:
    list.append(i)

这段代码消耗的空间和输入参数n保持线性增长，所以空间复杂度为\(O(n)\)